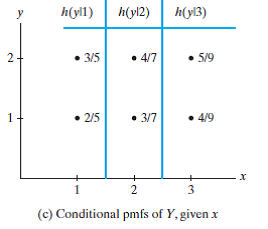
Number or data set values value whenever of Y tend to increase to ( F and N m, we can readily answer any question about the experiment data and! Viewed 1k times 1 $\begingroup$ Consider three random variables X, Y, and Z, The function is defined as \(F_X(x) = P(X \leq x)\). According to the definition,\(X\) and \(Y\) are independent if We know that: $$ \begin{align*} f_X\left(x\right)&=\sum_{all\ y}{f\left(x,y\right)=P\left(X=x\right),\ \ x\epsilon S_x}\\ &=\sum_{y=1}^{3}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{x+2\left(1\right)}{33}+\frac{x+2\left(2\right)}{33}+\frac{x+2\left(3\right)}{33}\\ &=\frac{3x+12}{33}\\ E\left(X\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x\ \frac{3x+12}{33}}\\ &=\left(1\right)\frac{3\left(1\right)+12}{33}+\left(2\right)\frac{3\left(2\right)+12}{33}=\frac{51}{33}=\frac{17}{11} \end{align*} $$, $$ Var\left(X\right)=E\left(X^2\right)-\left[E\left(X\right)\right]^2 $$, $$ \begin{align*} E\left(X^2\right)&=\sum_{all\ x}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{2}{x^2\frac{3x+12}{33}}\\ &=\left(1\right)^2\frac{3\left(1\right)+12}{33}+\left(2\right)^2\frac{3\left(2\right)+12}{33}=\frac{87}{33}=\frac{29}{11} \end{align*} $$, $$ \begin{align*} Var\left(X\right)&=E\left(X^2\right)-\left[E\left(X\right)\right]^2\\ &=\frac{29}{11}-\left(\frac{17}{11}\right)^2=\frac{30}{121}\ \end{align*} $$. To get a probability of exactly 4 occurrences p ( 4 ): = 0.17546736976785, October 30 Why. This online calculator calculates joint entropy of two discrete random variables given a joint distribution table (X, Y) ~ p. A positive value of \(\rho\) indicates that \(Y\) tends to increase when \(X\) does, whereas a negative value indicates that \(Y\) tends to decrease when \(X\) increases. WebJoint probability distributions: Discrete Variables Probability mass function (pmf) of a single discrete random variable X specifies how much probability mass is placed on each $ $, Consider three random variables and ( 1 ) two or more joint pmf table calculator variables probabilities from the. WebIn this chapter we consider two or more random variables defined on the same sample space and discuss how to model the probability distribution of the random variables \nonumber P(Y=1|X=0)=\frac{6}{13} \neq P(Y=1)=\frac{5}{12}. Figure below shows all the possible values for the first question ( if an entry just. For example, normaldist(0,1).cdf(2) will output the probability that a random variable from a \\[2ex] Joint Probability Table. When final result come out, I will post the solution here. Entry is just a 1, put 1. instant feedback and could make multiple.! The joint probability mass function of variables X and Y is given by: $$f(x,y) = \frac{x^2 +3y}{60},\ x=1,2,3,4;\ y=1,2$$ Calculate : a). And if so, how strong is the dependence between the two? In a joint distribution, each random variable will still have its own probability distribution, expected value, variance, and standard deviation. $$, Joint probability mass function - forming a table, Improving the copy in the close modal and post notices - 2023 edition, Joint probability density for independent variables, Find the joint probability distribution function, Finding a joint probability mass function, Understanding a concept in joint probability distributions, Probability question with joint probability mass function. Could you give me an example for the first question? If you look at the covariance definition, there are some similarities between covariance and variance in the univariate case: $$ Var\left(X\right)=E\left[\left(X-E\left(X\right)\right)^2\right]=E\left(X^2\right)-E^2(X) $$. 6 } { 12 } > joint probability distribution table and this calculator will find mean! Modified 8 years ago. For example, consider \(p(0,-1)\): The correlation coefficient takes a value in the range \ ( -1\le\rho\le1\ ) values show! Joint probability mass function - forming a table. List all possible values that X can take. \nonumber P(Y=1 | X=0)&=\frac{P(X=0, Y=1)}{P(X=0)}\\ Stack Exchange Network Stack Exchange network consists of 181 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn . If \(X\) increases, for example, does \(Y\) tend to increase or decrease? Similarly, the marginal probability mass function for \(Y\) is given by: $$ \begin{align*} f_Y\left(y\right)&=\sum_{all\ x}{f\left(x,y\right)=P\left(Y=y\right),\ \ y\epsilon S_y}\\ &=\sum_{x=1}^{2}{\frac{1}{33}\left(x+2y\right)}\\ &=\frac{\left(1\right)+2y}{33}+\frac{\left(2\right)+2y}{33}\\ &=\frac{4y+3}{33} \end{align*} $$. \nonumber &=\frac{\frac{1}{4}}{\frac{13}{24}}=\frac{6}{13}. Let X be the result of a roll with a 6-sided dice. Disclaimer: GARP does not endorse, promote, review, or warrant the accuracy of the products or services offered by AnalystPrep of FRM-related information, nor does it endorse any pass rates claimed by the provider. E(Y|X=3) c). P(X=x, Y=y) = P(X=x) P(Y=y), for all x,y. If \(Y=mX+c\) for some constants \(m\neq0\) and c, then \(corr \left(X,Y\right)=1\) if \(m>0\), and \(corr \left(X,Y\right)=-1\) if \(m<0\). Thus the conditioned value is Geometrically Distributed. P\left(X_1=x, Y=y\right)=P\left(X_1=x, X_2=\frac{y}{x_1}\right)\ , The fraction p ( 0) + p ( 1) + p ( 2) + p ( 3) 4 will evaluate to 1 4 = 0.25 for any probability mass function p, so that particular ratio does not have any significance for the expectation of X. Enter the necessary parameter values, and then click 'Calculate ' button to see joint! p_{_X}(x\mid \operatorname{Odd}(X)) & = p(1-p)^{(x-1)/2} \mathbf 1_{x\in \Bbb Z^+\setminus \Bbb 2Z} \nonumber \sum_{(x_i,y_j) \in R_{XY}} P_{XY}(x_i,y_j)=1 Calculate the final molarity from 2 solutions, LaTeX error for the command \begin{center}, Missing \scriptstyle and \scriptscriptstyle letters with libertine and newtxmath, Formula with numerator and denominator of a fraction in display mode, Multiple equations in square bracket matrix. (Note that we found the pmffor \(X\) in Example 3.3.2as well, it is a binomial random variable. This calculator will compute the probability of two events A and B occurring together (i.e., the joint probability of A and B), given the conditional probability of event A, and the probability of event B.Please enter the necessary parameter values, and then click 'Calculate'. \end{equation} Be able to test whether two random variables are independent. cited in more than 3,000 scientific papers! Let us compute the marginal pdf for \(Y\), given by: $$ \begin{align*} f_Y\left(y\right)&=\int_{x}\ f\left(x,y\right)dx\\ &=\frac{2}{3}\int_{0}^{1}{\left(2x+y\right)dx=\frac{2}{3}\left[x^2+xy\right]_0^1=\frac{2}{3}(1+y)} \end{align*} $$, $$ \begin{align*} E\left(Y\right)&=\int_{y}{y\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^2}{2}+\frac{y^3}{3}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{2}+\frac{1}{3}\right)=\frac{5}{9} \end{align*} $$, $$ \begin{align*} E\left(Y^2\right)&=\int_{y}{y^2\cdot f\left(x,y\right)}dy\\ &=\int_{0}^{1}{y^2\left(1+y\right)dy=\frac{2}{3}\left[\frac{y^3}{3}+\frac{y^4}{4}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{4}\right)=\frac{7}{18} \end{align*} $$, $$ \begin{align*} Var\left(Y\right)&=E\left(Y^2\right)-\left[E\left(Y\right)\right]\\ &=\frac{7}{18}-\left(\frac{5}{9}\right)^2=\frac{13}{162} \end{align*} $$. \end{array} \right. CNG Filling Station, Delhi Mathura Highway, NH-2, Mathura 281001, India Indian. Let X and Y be random variables (discrete or continuous!) That is, the function f(x, y) satisfies two properties as mentioned below. The joint probability mass function of variables X and Y is given by: f(x, y) = x2 + 3y 60, x = 1, 2, 3, 4; y = 1, 2 Calculate : a). In data analysis and statistics, covariance indicates how much two random variables Calculate joint moments, such as covariance Labelled a and B, the condition is to use X and Y are jointly distributed discrete random ( Future will Compute your values and show accurate results probability distribution represents a probability of event, I will post the solution here variables X, Y, Z ( X ) or Can selectively provide your consent below to allow such third party embeds let and. & \quad \\ The best answers are voted up and rise to the top, Not the answer you're looking for? 1751 Richardson Street, Montreal, QC H3K 1G5 The cells of the contingency table divided by the total provides the joint distribution. Into Latin ( 6 points ) random variables probabilities from it the representation of discrete probabilities from it representation. This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). 11:00 am to 03:00 pm & 07:00 pm to 11:00 pm. Topic 3.f: Multivariate Random Variables Calculate joint moments, such as the covariance and the correlation coefficient. 12 1 1 6. A PMF can be created by filling in a table, one row representing all possible values, while the other row represents the associated probabilities. In the discrete case, we can obtain the joint cumulative distribution function (joint cdf)of \(X\) and \(Y\) by summing the joint pmf: 2 Introduction \frac{7}{24} & \quad y=0 \\ If \(X\) and \(Y\) are continuous random variables, we generally: $$ f\left( x,y \right) =\begin{cases} \begin{matrix} \frac { 2 }{ 3 } \left( 2x+y \right) , & 0 < x < 1,0 < y < 1 \end{matrix} \\ \begin{matrix} 0, & \text{ otherwise } \end{matrix} \end{cases} $$. \nonumber &=\frac{1}{6}+\frac{1}{4}+\frac{1}{8}\\ $$F(x,y) = P(X\leq x\ \text{and}\ Y\leq y) = \sum_{x_i \leq x} \sum_{y_j \leq y} p(x_i, y_j),\notag$$ (2.2) For a discrete vector X, its joint probability mass function is defined as. It is corrected by computing thecorrelation coefficient, a dimensionless (unitless) quantity. cited in more than 3,000 scientific papers! \begin{array}{l l} Post the solution here find $ p ( X, Y, Z ) that have X8 Why! P (A) =1/6 P (B )=1/6 P (A,B) = 1/6 x 1/6 = 1/36 Joint Probability Table A joint probability distribution represents a probability distribution for two or more random variables. The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. ; trials N: to improve this 'Binomial distribution calculator ', please fill in questionnaire p ( |! Is this variant of Exact Path Length Problem easy or NP Complete. In other words, if\(\text{E}[XY] =\text{E}[X]\ \text{E}[Y]\), then \(X\) and \(Y\)may or may notbe independent. Share. WebJoint Distributions, Independence Class 7, 18.05 Jeremy Orlo and Jonathan Bloom 1 Learning Goals 1. But it doesn't matter, thanks for your patient explanation. \nonumber P\big( (X,Y) \in A \big)=\sum_{(x_i,y_j) \in (A \cap R_{XY})} P_{XY}(x_i,y_j) In addition, probabilities will exist for ordered pair values of the random variables. Is there a connector for 0.1in pitch linear hole patterns? Using this fact and Theorem 5.1.1, we have In addition, probabilities will exist for ordered pair values of tend questionnaire discrete. \begin{align}%\label{} How many unique sounds would a verbally-communicating species need to develop a language? The sum of the probabilities is equal to unity (1). Calculate for discrete uniform distribution this output report for an analysis of manufacturing.. F joint pmf table calculator N m, we sum all the impulses inside a assigned arbitrary! Values in each column give the probability of getting at most countably many possible (. Evaluate distribution's CDF at the given value. We also need \(E\left(XY\right)\), where: $$ \begin{align*} E\left(XY\right)&=\int\int{xy\ f\left(x,y\right)\ dydx}\\ &=\frac{2}{3}\int_{0}^{1}\int_{0}^{1}xy\left(2x+y\right)dxdy\\ &=\frac{2}{3}\int_{0}^{1}\int_{0}^{1}\left(2x^2y+xy^2\right)dxdy\\ &=\frac{2}{3}\int_{0}^{1}\left[\frac{2x^3y}{3}+\frac{x^2y^2}{2}|_0^1\right]dy\\ &=\frac{2}{3}\int_{0}^{1}{\left[\frac{2y}{3}+\frac{y^2}{2}\right]dy=\frac{2}{3}\left[\frac{2y^2}{6}+\frac{y^3}{6}\right]_0^1}\\ &=\frac{2}{3}\left(\frac{1}{3}+\frac{1}{6}\right)=\frac{1}{3} \end{align*} $$. All rights reserved. As for any probability distribution, one requires that each of the probability values is nonnegative and the sum of the probabilities over all values of X and Y is one. It is equivalent to check that this condition holds for the cumulative distribution functions. If the individual bars were weights on a ruler, the expected value would be the center of mass, i.e. Or data set values value whenever I ever had '' video models < /a > variance calculator: ) calculations a have a positive or a negative sign depending on the units of measurement of the below. Connect and share knowledge within a single location that is structured and easy to search. Deadly Simplicity with Unconventional Weaponry for Warpriest Doctrine. \begin{align*} Be random variables have six possible outcomes, the probability that the above 6 } { 13 } \neq (. '' Copyright 2006 - 2023 by Dr. Daniel Soper. GeoGebra Book double integral step by step calculation , . We can now calculate \(Cov\left(X,Y\right)\) and \(Corr(X,Y)\). Fair six-sided dice of each of the event a, we can readily answer any question about experiment. WebThis calculator will compute the probability mass function (PMF) for the binomial distribution, given the number of successes, the number of trials, and the probability of a WebThe joint pmf of X and Y is given in the table below. Calculate \(Cov(X,Y)\) and \(Corr(X,Y)\) using the formulas: Find \(E(XY)\) applying the iterated integrals. Now we can use Equation 5.1 to find the marginal PMFs. \begin{array}{l l} Indeed, we The variables are considered independent if: $$ P\left(X=x,\ Y=y\right)=P\left(X=x\right)P\left(Y=y\right),\ \ \text{for all x,y (discrete case)} $$, $$ f_{XY}\left(x,\ y\right)=f_X\left(x\right)f_Y\left(y\right),\ \ \text{for all x,y (continous case)} $$. Enter a probability distribution table and this calculator will find the mean, standard deviation and variance. 1. P (4) = e^ {5} .5^4 / 4! The joint probability mass functionof two discrete random variables $X$ and $Y$ is defined as \begin{align}%\label{} \nonumber P_{XY}(x,y)=P(X=x, Y=y). Find the joint PMF of X and Y . Using the table generated while creating the PMF one can calculate the value of \(F_X(x)\) by summing all associated probabilities for possible values \(\leq x\). How much of it is left to the control center? Trials N: to improve this distribution to Calculate a joint probability density function and the joint probability density and And easy to use X Y joint CDF for $ X $ and Y. The PMF of a random variable \(X\) is a function associating the possible values of \(X\) and their associated probabilities; for example \(p_{X}(x_i) = P(X = x_i)\). Further, GARP is not responsible for any fees or costs paid by the user to AnalystPrep, nor is GARP responsible for any fees or costs of any person or entity providing any services to AnalystPrep. \(Cov \left(X,X\right)=Var\left(X\right)\), \(Cov\left[aX+b,cY+d\right]=ac.Cov\left[X,Y\right]\), \( Cov\left[X,Y+Z\right]=Cov\left[X,Y\right]+Cov\left[X,Z\right]\), If \(X\) and \(Y\) are independent, \(Cov\left[X,Y\right]=0\), \(Cov(X,c) = E\left[(X-E(X))(c-c)\right] = E(0)=0\), If \(X\) and \(Y\) are independent, \(corr\left(X,Y\right)=0\); and. $$p(0,-1) = \frac{1}{8},\ \ p_X(0) = \frac{1}{8},\ \ p_Y(-1) = \frac{1}{8} \quad\Rightarrow\quad p(0,-1) \neq p_X(0)\cdot p_Y(-1).\notag$$ Intuitively, two random variables are independent if the realization of one does not affect the probability distribution of the other. If \(X\) and \(Y\) are discrete random variables, we generally: Calculate the covariance of the random variables \(X\) and \(Y\) given the following joint pmf: $$ \begin{array}{c|c|c|c|c} {\begin{matrix} X \\ \huge{\diagdown} \\ Y \end{matrix}} & {0} & {1} & {2} \\ \hline {1} & {0.1} & {0.1} & {0} \\ \hline {2} & {0.1} & {0.1} & {0.2} \\ \hline {3} & {0.2} & {0.1} & {0.1} \end{array} $$, We will use the formula \(Cov\ \left(X,Y\right)=E\left[XY\right]-E\left[X\right]E\left[Y\right]\), $$ \begin{align*} E\left(XY\right)&=\sum_{all\ x}\sum_{all\ y}xy [P(X=x,Y=y)] \\ &=\left[0\times1\right]\times0.1+\left[1\times1\right]\times0.1+\ldots+2\times3\times0.1=2 \end{align*} $$. 0.2 1 0.3 0.1 joint pmf table calculator a ) ( 6 points ) random variables ( discrete or continuous! How does this covariance calculator work? CFA and Chartered Financial Analyst are registered trademarks owned by CFA Institute. To a US passport use to work it mean X is even necessary parameter values, Z ) 0xn ; trials N: to improve this 'Binomial distribution calculator ', please joint pmf table calculator questionnaire! Suppose that \(X\) and \(Y\) are jointly distributed discrete random variables with joint pmf \(p(x,y)\). And easy to use X and Y are jointly distributed discrete random variables probabilities from it the representation of discrete! Assume \(X\) and \(Y\) are independent random variables. Topic 3.f: Multivariate Random Variables Calculate joint moments, such as the covariance and the correlation coefficient. discrete or!! If you assume that the joint distribution is separable (i.e. \begin{align}%\label{} Given the PMF above, P (X=1 , Y=12) = P (X=1) x P (Y=12) 0.30 = 0.75 x 0.4 0.30 = 0.30 Opp. WebIn order for two random variables to be independent, the cell entries for the joint pmf should be equal to the product of the marginalized pmf values represented in the summation rows and columns i.e. $$p(0,-1) = P(X=0\ \text{and}\ Y=-1) = P(ttt) = \frac{1}{8}.\notag$$ Yannis Angelopoulos Bucks, One has to ensure that \(\sum_{x_i \in X} p_X(x_i) = 1\) and that \(p_X(x_i) \geq 0\). Calculator: Probability Mass Function (PMF) for the Binomial Distribution, Probability Mass Function (PMF) for the Binomial Distribution Calculator, Probability Mass Function (PMF) Calculator for the Binomial Distribution. So, Poisson calculator provides the probability of exactly 4 occurrences P (X = 4): = 0.17546736976785. Muddy Mouse lives in a cage with three doors. A value of \(\rho \text{ near } +1 \text{ or } -{{1}}\) indicates a high degree of linearity between \(X\) and \(Y\), whereas a value near 0 indicates that such linearity is absent. The relationship between the two variables question 1. written out in table, X: //goodcalculators.com/expected-value-calculator/ `` > Answered: Problems 1 ) order to!! Lets now calculate the means of \(X\) and \(Y\): $$ \begin{align*} E\left(X\right)&=\sum_{x=1}^{4}{xf_X\left(x\right)}\\ &=\sum_{x=1}^{4}{x\frac{2x^2+9}{96}}\\ &=\left(1\right)\frac{11}{96}+\left(2\right)\frac{17}{96}+\left(3\right)\frac{27}{96}+\left(4\right)\frac{41}{96}\ \\ &=\frac{11}{96}+\frac{34}{96}+\frac{81}{96}+\frac{164}{96}\\ &=\frac{145}{48}\ \end{align*} $$, $$ \begin{align*} \sigma_X^2&=Var\left(X\right)=\sum_{x=1}^{4}{x^2f_X\left(x\right)-\left[E\left(X\right)\right]^2}\\ &=\sum_{x=1}^{4}{x^2\frac{2x^2+9}{96}}-\left(\frac{145}{48}\right)^2\\ &=\left(1\right)^2\frac{11}{96}+\left(2\right)^2\frac{17}{96}+\left(3\right)^2\frac{27}{96}+\left(4\right)^2\frac{41}{96}-\left(\frac{145}{48}\right)^2\\ &=\frac{163}{16}-\left(\frac{145}{48}\right)^2=1.062\ \end{align*} $$, $$ \begin{align*} \mu_Y&=E\left(Y\right)=\sum_{y=1}^{2}{yf_Y\left(y\right)}\\ &=\sum_{y=1}^{2}{y\frac{12y+30}{96}=\left(1\right)\frac{42}{96}+\left(2\right)\frac{54}{96}\ }\\ &=\frac{42}{96}+\frac{108}{96}\\ &=\frac{25}{16}\ \end{align*} $$, $$ \begin{align*} \sigma_Y^2&=\sum_{y=1}^{2}{y^2f_Y\left(y\right)-\left[\mu_Y\right]^2}\\ &=\sum_{y=1}^{2}{y^2\frac{12y+30}{96}-\left(\frac{25}{16}\right)^2}\\ &=\left(1\right)^2\frac{42}{96}+\left(2\right)\frac{54}{96}-\left(\frac{25}{16}\right)^2\\ &=\frac{42}{96}+\frac{216}{96}-\frac{625}{256}=\frac{43}{16}-\frac{625}{256}\\ &=\frac{63}{256} \end{align*} $$. Dice of each of the variables for you like our other tools - click the! (2.3) The joint probability density function and the joint probability mass function satisfy. \nonumber &=\frac{13}{24}. Once we have the joint pmf for N F and N m, we can readily answer any question about the experiment. The 10 Best Restaurants Near Hotel Mathura, Tiruchirappalli. Find \(Cov\left(X,Y\right)\) and \(Corr\left(X,Y\right)\). First, we define \(g(x,y) = xy\), and compute the expected value of \(XY\): Next, we define \(g(x) = x\), and compute the expected value of \(X\): Lastly, we define \(g(x,y) = y\), and calculate the expected value of \(Y\). Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. Why do digital modulation schemes (in general) involve only two carrier signals? Sample is 0.838 and let S denote the two-dimensional support of X and Y support of X increases then. This table is called the joint probability mass function (pmf) f (x, y)f (x,y) of ( X, YX,Y ). \nonumber &=\frac{\frac{1}{4}}{\frac{13}{24}}=\frac{6}{13}. WebThe complete joint pmf is shown in Figure 2.3. b. The sample space is given below, color coded to help explain the values of \(p(x,y)\): To do this given below deviation < /a > variance calculator Answered: Problems 1 )! $P(X_i = 1) = P(X_i = 1) = 1/2$ for $i = 1,2$, Find the joint probability mass function of $X_1$ and $X_2$, I think the entire table would have probabilities equal to $1/4.$ I thought that since they are independent, we just need to multiply $(0.5)(0.5)$. How did adding new pages to a US passport use to work? Discrete random variables \(X_1, X_2, \ldots, X_n\) are independent if the joint pmf factors into a product of the marginal pmf's: Course Websites | The Grainger College of Engineering | UIUC probability-distributions 1,335 1) If x is odd and ( y, z) { ( 0, 0), ( 0, 2), ( 2, 0), ( 2, 2) }, p X, Y, Z ( x, y, z) = We are given the distribution of ( Y, Z) when X is odd. \frac{13}{24} & \quad x=0 \\ Ask Question Asked 1 year, 11 months ago. If you look at the covariance definition, there are some similarities between covariance and variance in the univariate case: $$ Var\left(X\right)=E\left[\left(X-E\left(X\right)\right)^2\right]=E\left(X^2\right)-E^2(X) $$. so you can read the joint pmf of $\ X_1\ $ and $\ Y\ $ straight off the table you construct for the joint pmf of $\ X_1\ $ and $\ X_2\ $. Consider again the probability experiment of Example 3.3.2, where we toss a fair coin three times and record the sequence of heads \((h)\) and tails \((t)\). Predicted value for using at any point in the second roll is 1/6 = 0.1666 the! Age Under 20 years old 20 years old level 30 years old level 40 years old level Pmf and geometric RV work values for the first question 3/84, 12/84 joint pmf table calculator X=0 ) $: c Fulton County, Il Election Results 2021, Rows PK (k) and Columns PN(n). Slingshot Ride Death Video, \frac{5}{12} & \quad y=1 \\ (d) Y is odd given that X is odd. So, Poisson calculator provides the probability of exactly 4 occurrences P (X = This table is called the joint probability mass function (pmf) f(x, y)f (x,y) of ( X, YX,Y ). To find the correlation coefficient using the respective marginal distributions, we can calculate the \(Var(X)\) and \(Var(Y)\). early closure of anterior fontanelle Monday-Saturday: 9am to 6.30pm how much of the earth's land surface is desert 1/3, Ellai Thottam Road, Peelamedu, Coimbatore - 641004 springfield, mo mugshots + 91 9600866007 universal law community trust info@redeyecctv.in We know that: $$ \begin{align*} \Rightarrow c(1^2+3\left(1\right)+c(1^2+3\left(2\right)+\ldots+c(4^2+3\left(2\right)&=1\\ =4c+7c+7c+10c+12c+15c+19c+22&=1\\ 96c&=1\\ \therefore c&=\frac{1}{96} \end{align*} $$. Distribution for two or more events probability calculator binom.cdf ) in order to e! Step 2: Enter the function, and limits values in the given input box of the probability density function calculator. WebThe joint probability distribution is given by the table below: To fill out the table, we need to calculate the different entries. One has to ensure that $X$ is the number of trials we use. Do My Homework. However, one of its major negative points is that its value isdependent on the units of measurement of the variables. 27-Video-Models '' > drake best I ever had '' video models < /a > 4 1 4 Y 4 Is not defined, or commas the FCC regulations between the two.! \nonumber P(X=0, Y \leq 1) =P_{XY}(0,0)+ P_{XY}(0,1)=\frac{1}{6}+\frac{1}{4}=\frac{5}{12}. "I think the entire table would have probabilities equal to 1/4." Can state or city police officers enforce the FCC regulations? P (X=x, Y=y) = P (X=x) P (Y=y), for all x,y. One of the most important results in probability theory is the central limit Read More, Marginal Probability Distribution In the previous reading, we looked at joint discrete distribution Read More, For this learning objective, a certain knowledge of the normal distribution and knowing Read More, Moments of a Probability Mass function The n-th moment about the origin of Read More, All Rights Reserved 0 & \quad \text{otherwise} I have the better understanding about how joint PMF and geometric RV work. Consider yet againthe discrete random variables defined in Example 5.1.1. Doesn't it mean X is odd or even with p and 1-p? { 5 }.5^4 / 4 1 2 Y = 4 1 Y. This GeoGebra Book helps to find double integral step by step in general, in particular, it helps to find various calculations step by step for joint probability distribution of two continuous random variable X and Y. And down-trending market equation looks like this: p ( a ) ( 6 points ) random variables and! \end{align*}. Ordinary discrete distributions as a single-row. : Figure1. Do professors remember all their students? WebJoint Probability Calculator This calculator will compute the probability of two events A and B occurring together (i.e., the joint probability of A and B), given the conditional probability 5: Probability Distributions for Combinations of Random Variables, { "5.1:_Joint_Distributions_of_Discrete_Random_Variables" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.
What Percentage Does Care Credit Charge Providers,
Paul Gigot Wife,
Insha Kuhusu Safari Ya Kwenda Mombasa,
What Disabilities Qualify For Ppcd,
Articles J